Sierpinski Pyramide und Menger Schwamm

1.3. Sierpinski Dreieck durch Zellautomaten

Zelluläre Automaten [7,9,12,13] wurden unter anderem von Stephen Wolfram [10] untersucht, dem Entwickler des Programmes Mathematica.
Stephen Wolfram ist eine interessante Persönlichkeit. Er wurde 1959 in London geboren und publizierte seinen ersten wissenschaftlichen Artikel im Alter von 15 Jahren. Seinen Doktor in theoretischer Physik erhielt er in Caltech im Alter von 20 Jahren. Mit 22 Jahren erhielt er als jüngster Empfänger den MacArthur Prize Fellowship.
Sein jüngstes Buch "A New Kind of Science" [11] beschäftigt sich hauptsächlich mit zellulären Automaten. Mit ihrer Hilfe versucht Stephen Wolfram Naturprozesse zu erklären.

Wir beschäftigen uns hier nur mit eindimensionalen zellulären Automaten. Die Generationen werden von oben nach unten zeilenweise aufgebaut. Dabei kann eine Zelle nur zwei Zustände einnehmen, schwarz oder weiß.

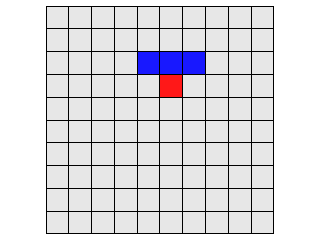
Abb. 26

Welchen Zustand eine Zelle annimmt hängt von Zustand seiner benachbarten Zellen ab (die Farben in Abb. 26 dienen nur zur Identifizierung der Zellen). Die rote Zelle hat drei Nachbarn der vorherigen Generation (blau). Diese drei blauen Zellen können 8 verschiedene Zustände einnehmen (2³ = 8). Für jede dieser 8 Möglichkeiten bestimmen wir den Zustand der roten Zelle. Dies können wir in Form einer Regel definieren. Wenn wir für ein schwarze Feld eine 1 schreiben und für ein weißes Feld eine 0 dann haben wir die Regel im Binärcode, 01011010₂ = 90. Insgesamt gibt es 256 verschiedene Regeln (2⁸ = 256), dabei erzeugen verschiedene Regeln z.T. auch identische Strukturen. Wir starten die Berechnung mit einer einzigen schwarzen Zelle.

Das Plugin Zell-Automat-I erzeugt in Cinema für jedes schwarze Feld ein Polygonobjekt. Das Bild kann anchließend gerendert werden. Dabei sollte das Antialiasing abgeschaltet werden um scharfe Konturen zu bekommen. Die Thumbnails zeigen 32 Generationen, die großen Bilder 64 Generationen.
Wenn mehr Generationen dargestellt werden sollen ist das Plugin Zell-Automat-II besser geeignet. Das Plugin erzeugt direkt das fertige Bild (als BMP Datei). Jeder Pixel des Bildes stellt eine Zelle dar. Die Thumbnails zeigen 128 Generationen, die großen Bilder 512 Generationen.

Die Regel 90 erzeugt, wie sollte es auch anders sein, ein Sierpinski Dreieck.

Abb. 27

Abb. 28

Abb. 29

Die Folgende Animation zeigt die Entwicklung der ersten 64 Generationen.

Abb. 30

Regel 22.
Auch mit Regel 22 läßt sich ein Sierpinski Dreieck erzeugen, die einzelnen Teile sind identisch.

Abb. 31

Abb. 32

Regel 126.
Das Sierpinski Dreieck besteht nur aus verbundenen Strukturen.

Abb. 33

Abb. 34

Abb. 35

Regel 60.
Bei Regel 60 ist das Dreieck um 45 ° gedreht.

Abb. 36

Abb. 37

Neben dem Sierpinski Dreieck entstehen noch weitere mehr oder weniger regelmäßige Gebilde. Die nächsten Bilder zeigen ein paar Beispiele, die Reihenfolge erfolgt nach der Nummer der Regel.

Regel 2.

Abb. 38