[zurück]

1.2. Sierpinski Dreieck durch Zufall

[vor]

Das Sierpinski Dreieck läßt sich auch durch einen Zufallsalgorithmus (Chaos Game) [20,21] erzeugen. Dazu brauchen wir nur die 3 Eckpunkte des Dreiecks und einen Würfel.

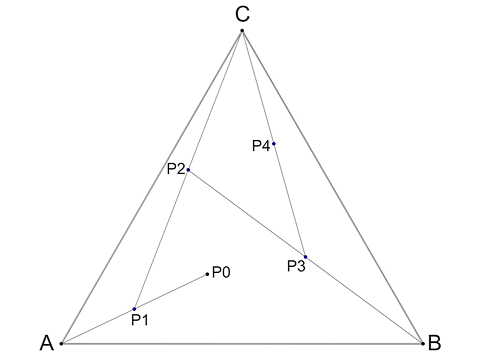
Abb. 16

Wir setzen irgendwo einen Punkt in das Dreieck als Startpunkt (P0).
Dann würfeln wir ein A und ziehen eine Linie von P0 zu A. In die Mitte dieser Linie setzen wir einen Punkt (P1).
Dann würfeln wir ein C und ziehen eine Linie von P1 zu C. In die Mitte dieser Linie setzen wir einen Punkt (P2).
Dann würfeln wir ein B und ziehen eine Linie von P2 zu B. In die Mitte dieser Linie setzen wir einen Punkt (P3).
Dann würfeln wir ein C und ziehen eine Linie von P3 zu C. In die Mitte dieser Linie setzen wir einen Punkt (P4).

Das machen wir jetzt ein paar Tausend mal und schauen was dabei herauskommt.

Die folgende Animation zeigt die Entwicklung des Sierpinski Dreiecks (100 Punkte bis 1000000 Punkte in 20 Stufen).

Abb. 17

Abb. 18 zeigt das Sierpinski Dreieck mit 1000000 Punkten. Die Größe der Punkte wurde wegen der feinen Struktur relativ klein gewählt.

Abb. 18

Wie beim Dreieck läßt sich dieses Berechnungsschema auch auf andere n-Ecke übertragen. Beim Viereck bekommen wir ein Ergebnis das eigentlich auch beim Dreieck zu erwarten war, die Punkte bilden ein statistisch verteiltes Rauschen.

Abb. 19

Beim Fünfeck bekommen wir wie beim Dreieck scharfe Strukturen. Im Bild sind verschieden große Fünfecke zu erkennen.

Abb. 20

Beim Sechseck erhalten wir ein System feiner Linien.

Abb. 21

Wenn wir die Punkte kleiner machen kommt die Struktur besser zur Geltung.

Abb. 22

Beim Siebeneck erhalten wir ein Loch in der Mitte und ein paar helle Strukturen. Ob das Loch ein Siebeneck wird läßt sich bei 1000000 Punkten nicht erkennen.

Abb. 23

Beim Achteck erhalten wir nur ein diffuses Loch in der Mitte.

Abb. 24

Beim Neuneck erhalten wir wieder ein Loch in der Mitte. Ob das Loch ein Neuneck wird läßt sich bei 1000000 Punkten nicht erkennen.

Abb. 25

[zurück]

[Inhaltsverzeichnis]

[vor]