| [zurück] | Das Sierpinski Dreieck |
[vor] |
Die fraktale Dimension D [2] oder Hausdorff Dimension wurde von Felix Hausdorff (1868 - 1942) 1919 eingeführt. Sie ist wie folgt definiert.
|
|
10-14 |
|
|
|
10-15 |
Gl. 10-15 können wir auch anders schreiben.
|
|
10-16 |
Für das Sierpinski Dreieck ist a=3 und v=2. Wenn wir die Seitenlänge des Sierpinski Dreiecks verdoppeln erhalten wir 3 neue Dreiecke (Teile).
|
|
10-17 |
Das Sierpinski Dreieck hat also eine fraktale Dimension von 1,5850. Um das zu verstehen betrachten wir die Dimensionen normaler geometrischer Objekte.
Wenn wir eine Stecke verdreifachen (v=3), erhalten wir 3 Teile (a=3).
![]()
Abb. 2
Die Dimension ist 1, bei einer Stecke oder Linie handelt es sich um ein eindimensionales Objekt.
|
|
10-18 |
Wenn wir die Kantenlänge eines Quadrats verdreifachen (v=3), erhalten wir 9 Teile (a=9).
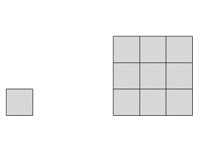
Abb. 3
|
|
10-19 |
Die Dimension ist 2, bei einem Quadrat handelt es sich um ein zweidimensionales Objekt, eine Fläche.
Wenn wir die Kantenlänge eines Würfels verdreifachen (v=3), erhalten wir 27 Teile (a=27).
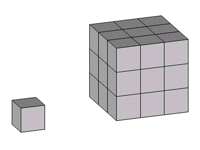
Abb. 4
|
|
10-20 |
Die Dimension ist 3, bei einem Würfel handelt es sich um ein dreidimensionales Objekt, einen Körper.
Das Sierpinski Dreieck mit einer fraktalen Dimension von 1,5850 liegt zwischen einer Linie und einer Fläche.
| [zurück] | [Inhaltsverzeichnis] | [vor] |