| [zurück] | 1. Das Sierpinski Dreieck |
[vor] |
Das Sierpinski Dreieck [1,8] wurde nach dem polnischen Mathematiker Waclaw Sierpinski (1882 - 1969) benannt. Es entsteht aus einem gleichseitigen Dreieck das nach bestimmten Regeln unterteilt wird.
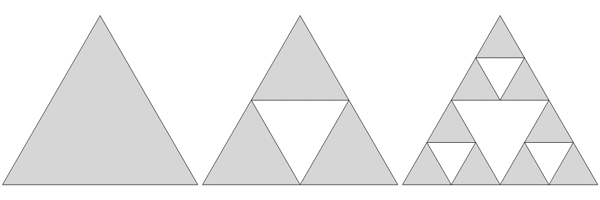
n=0![]() n=1
n=1![]() n=2
n=2
Abb. 1
Dabei werden die Seiten in der Mitte geteilt. Aus den einstandenen 3 Punkten wird ein neues Dreieck gebildet und entfernt. So entstehen aus dem ursprünglichen Dreieck (Stufe 0) 3 neue Dreiecke (Stufe 1). Jedes dieser 3 Dreiecke wird nach diesem Schema weiter unterteilt (Stufe 2).
Für die Stufe oder den Grad n erhalten wir N Dreiecke.
|
|
10-1 |
Interessant wird es wenn wir den Umfang und den Flächeninhalt der Dreiecke verfolgen. Bezeichnen wir die Kantenlänge des ersten Dreiecks (Stufe 0) mit a so erhalten wir folgende Formeln für den Umfang
|
|
10-2 |
und den Flächeninhalt.
|
|
10-3 |
Da die Fläche in jeder Stufe in 4 Teile geteilt wir von dem ein Teil verworfen wird beträgt die neue Fläche nur 3/4 der alten Fläche. So können wir für die verschiedenen Stufen eine Formel herleiten.
|
|
10-4 |
|
|
|
10-5 |
|
|
|
10-6 |
Für die Fläche der Stufe n können wir auch allgemein schreiben
|
|
10-7 |
Für den Umfang gilt Ähnliches, der Umfang vergrößert sich um den Faktor 3/2.
|
|
10-8 |
|
|
|
10-9 |
|
|
|
10-10 |
Für den Umfang der Stufe n können wir auch allgemein schreiben
|
|
10-11 |
Berechnen wir die Fläche und dem Umfang des Sierpinski Dreiecks für verschiedene Stufen.
| Stufe n | Fläche | Umfang |
| 0 | A0 | U0 |
| 1 | 0,75 A0 | 1,50 U0 |
| 2 | 0,56 A0 | 2,25 U0 |
| 5 | 0,24 A0 | 7,59 U0 |
| 10 | 0,056 A0 | 57,67 U0 |
| 20 | 0,0032 A0 | 3325,26 U0 |
| 30 | 0,00018 A0 | 191751, 06 U0 |
Wie wir sehen nimmt die Fläche mit zunehmender Unterteilung stark ab während der Umfang immer größer wird. Dies können wir auch mathematich erklären indem wir für die Fläche und den Umfang den Grenzwert (limes) bestimmen.
|
|
10-12 |
|
|
|
10-13 |
Dieses Ergebnis können wir ebenfalls in die Tabelle eintragen.
| Stufe n | Fläche | Umfang |
| 0 |
Wir haben also ein Objekt dessen Fläche mit zunehmendem Umfang immer kleiner wird. Das widerpricht der klassischen euklidischen Geometrie.
Beim Sierpinski Dreieck handelt es sich um fraktale Geometrie. Um solche Objekte besser beschreiben zu können hat man den Begriff der fraktalen Dimension eingeführt. Mehr dazu auf der nächsten Seite.
| [zurück] | [Inhaltsverzeichnis] | [vor] |