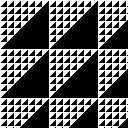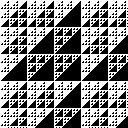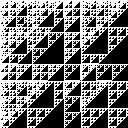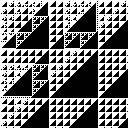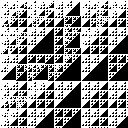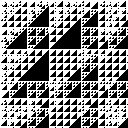Die Idee zu diesem Plugin habe ich auf der Seite von Manfredissimo [15] gefunden der diesen Algorithmus als Java Applet umgesetzt hat. Die Regel dazu ist eigentlich ganz einfach. In einem quadratischen Raster wird die oberste Zeile und die linke Spalte mit Einzen gefüllt. Die anderen Zellen werden jeweils aus der Summe des linken Nachbarn und des oberen Nachbarn gebildet (siehe Abb. 90).
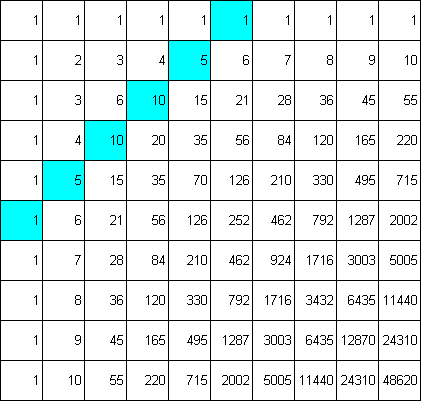
Abb. 90
Wir erhalten die Zahlen des Pascal´schen Dreiecks in Form der Diagonalen (ein Beispiel blau markiert).
Zur Erzeugung der Bilder prüfen wir die Teilbarkeit aller Zahlen mit der Modulo Funktion. Ist eine Zahl glatt teilbar wird die Zelle eingefärbt. Für verschiedene Teiler erhalten wir sehr unterschiedliche Bilder die meistens an das Sierpinski Dreieck erinnern.
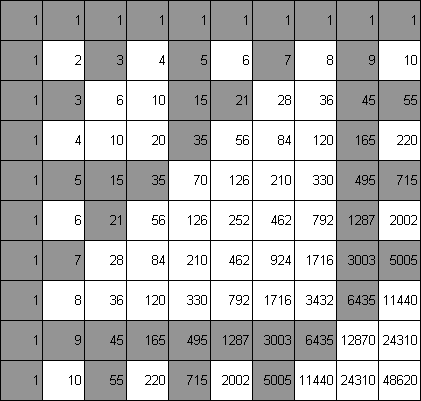
Abb. 91
Diesen Algorithmus in Coffee umzusetzten erschien eigenlich einfach. Wir haben aber das gleiche Problem wie mit dem Reiskorn auf dem Schachbrett, schon nach kurzer Zeit werden die Zahlen so groß das sie den Wertebereich für Integer Zahlen überschreiten. Dieses Problem läßt sich zwar lösen aber die Berechnung dauert dann sehr lange, bei 512 Pixel Kantenlänge etwa 3 Stunden (1,33 GHz Athlon). Coffee ist für solchen Berechnungen einfach nicht geeignet.
Die folgenden Abbildungen zeigen Bilder mit verschiedenen Teilern (2 bis 21). Die kleinen Bilder haben eine Kantenlänge von 128 und die großen Bilder eine Kantenlänge von 512.
| Mod 2 |
 |
Mod 3 |
 |
Mod 4 |
 |
Mod 5 |
 |
 |
 |
 |
 |
 |
 |
| Abb. 92 |
 |
Abb. 93 |
 |
Abb. 94 |
 |
Abb. 95 |
| Mod 6 |
 |
Mod 7 |
 |
Mod 8 |
 |
Mod 9 |
 |
 |
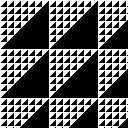 |
 |
 |
 |
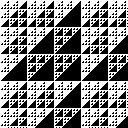 |
| Abb. 96 |
 |
Abb. 97 |
 |
Abb. 98 |
 |
Abb. 99 |
| Mod 10 |
 |
Mod 11 |
 |
Mod 12 |
 |
Mod 13 |
 |
 |
 |
 |
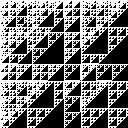 |
 |
 |
| Abb. 100 |
 |
Abb. 101 |
 |
Abb. 102 |
 |
Abb. 103 |
| Mod 14 |
 |
Mod 15 |
 |
Mod 16 |
 |
Mod 17 |
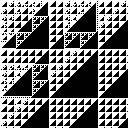 |
 |
 |
 |
 |
 |
 |
| Abb. 104 |
 |
Abb. 105 |
 |
Abb. 106 |
 |
Abb. 107 |
| Mod 18 |
 |
Mod 19 |
 |
Mod 20 |
 |
Mod 21 |
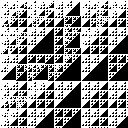 |
 |
 |
 |
 |
 |
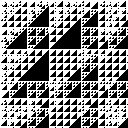 |
| Abb. 108 |
 |
Abb. 109 |
 |
Abb. 110 |
 |
Abb. 111 |