3.5. Der umstülpbare Würfel
|
[zurück] | 3.5. Der umstülpbare Würfel |
[vor] | |
Bei diesem Beispiel handelt es sich um den umstülpbaren Würfel nach Paul Schatz.
Die mathematiche Theorie dazu gibt es von Franz Zahaurek. Wer mehr über Paul Schatz (1898 - 1979) wissen möchte findet genug Informationen bei der Paul Schatz Stiftung.
Um zum umstülpbaren Würfel zu kommen muß ein Würfel in 3 Teile zerschnitten werden, in den Würfelgürtel und die zwei Riegelkörper. Das Volumen des Würfelgürtels beträgt 1/3 des Würfels.
Auch bei den Proportionen der Dreiecke spielt die Zahl 3 eine große Rolle.
Die erste Animation zeigt das Entfernen der beiden Riegelkörper.
Die Bildgröße beträgt 352*288 Pixel, das Format ist MPEG1.
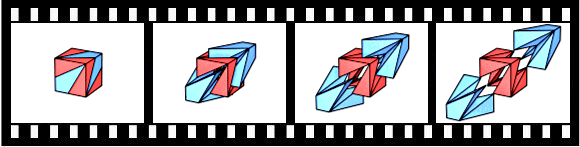
Die zweite Animation zeigt die Drehung des Würfels. Die unterschiedliche Texturierung dient nur zu besseren Übersicht, alle 6 Tetraeder sind gleich.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |