Lemniskate
|
[zurück] | Lemniskate |
[vor] | |
Die Gleichung der Lemniskate lautet.
|
x4 + y4 + 2 * x2 * y2 = 2 * a2 * (x2 – y2) |
1-22 |
In dieser Form läßt sich die Kurve aber nicht darstellen. Wir benötigen die Parameterdarstellung.
|
X(t) = a * cos(t) / (1 + (sin(t))2) |
1-23 |
|
|
Y(t) = a * sin(t) * cos(t) / (1 + (sin(t))2) |
1-24 |
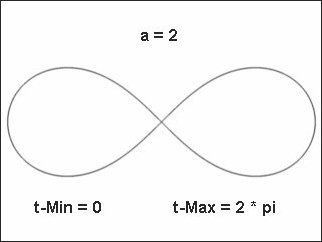
Abb. 5
Der Definitionsbereich beträgt 0 <= t<= 2 pi um eine geschlossenen Kurve darzustellen. Wenn t größer als 2 pi ist werden mehrere Kurven übereinander gezeichnet. Werden diese Kurven in Z Richtung auseinandergezogen so erhält man ein interessantes Schleifenmuster.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |