| [zurück] | Einführung |
[vor] |
Eine Kurvenlinie wird in der Regel durch eine Funktionsgleichung beschrieben. In einer X Y Ebene wird dieser Zusammenhang durch eine Funktion
|
y = f(x) |
1-1 |
beschrieben. Für jede Variable x erhält man in der Regel einen Wert y. Aber nicht jeder Zusammenhang läßt sich durch so eine explizite Form darstellen. Abhilfe schafft dann manchmal die Parameterdarstellung. Dabei wird der Zusammenhang durch zwei Funktionsgleichungen dargestellt.
|
x = f1(t) |
1-2 |
|
|
y = f2(t) |
1-3 |
Für jeden Wert von t erhält man einen x und einen y Wert und damit einen Punkt auf der XY Ebene. Die Parameter t legt den Definitionsbereich (tMin < t < tMax) der Funktion fest.
Den Unterschied zwischen Funktionsgleichung und Parameterdarstellung möchte ich am Beispiel der Kreisgleichung erläutern. Ein Kreis wird durch die Gleichung
|
x2 + y2 = r2 |
1-4 |
definiert. Der Kreismittelpunkt befindet sich dabei am Koordinatenursprung (0,0). Diese Gleichung entspricht aber nicht der gewohnten Form y = f(x), sie läßt sich aber in diese Form umwandeln indem wir sie umstellen und nach y auflösen.
|
y2 = r2 - x2 |
1-5 |
|
|
y = sqrt(r2 - x2) |
1-6 |
Diese Funktion ist nur definiert für den Bereich - r <= x<= r da aus einer negativen Zahl keine Quadratwurzel gezogen werden kann.
Die Parameterdarstellung des Kreises lautet
|
X(t) = r * sin(t) |
1-7 |
|
|
Y(t) = r * cos(t) |
1-8 |
Der Definitionsbereich beträgt 0 <= t<= 2 pi um einen geschlossenen Kreis darzustellen. Wenn t größer als 2 pi ist werden mehrere Kreise übereinander gezeichnet.
Beide Funktionen (1-6 und 1-7/8) ergeben den gleichen Kurvenverlauf.
Diese Parameterdarstellung von Funktionsgleichungen läßt sich auch mit Cinema 4D nutzen um komplexe Kurven zu erzeugen (Menü Objekte - Splines - Formel).
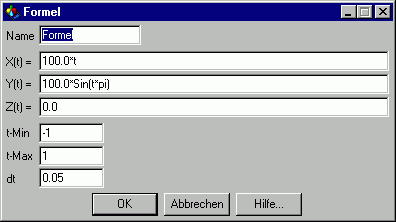
Abb. 1
Aber nun Schluß mit der Theorie und wir widmen uns einigen praktischen Beispielen.
| [zurück] | [Inhaltsverzeichnis] | [vor] |