[zurück]

Auto 2

[vor]

Die erste Version meines Autos hatte noch ein paar Fehler, so drehten sich die Räder in die falsche Richtung wenn das Auto rückwärts fuhr. Ausserdem drehten sich die Räder wenn man das Auto quer zur Fahrtrichtung bewegte.
Beide Fehler habe ich jetzt beseitigt.

Das erste Problem ist wie bringen wir dem Auto bei das es weiss in welche Richtung es fährt. Dazu benutzen wir das Objektachsensystem des Autos, eine Achse zeigt ja immer in Fahrtrichtung. Den entsprechenden Vektor entnehmen wir der lokalen Matrix des Autos die wir in Vektoren umwandeln. In unserem Auto zeigt V3 in Fahrtrichtung (blauer Pfeil).

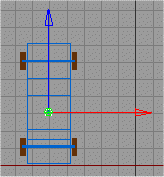
Wenn wir das Auto drehen ändert sich der Vektor V3.

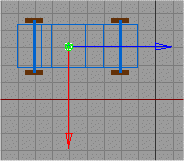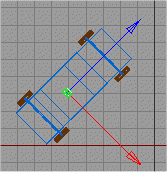
H = 0°	H = -45°	H = -90°
V3 = (0; 0; 1)	V3 = (0,707; 0; 0,707)	V3 = (1; 0; 0)

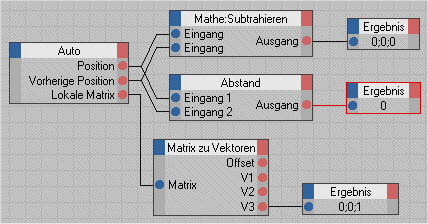
Aus der Position des Autos und der Vorherigen Position erzeugen wir durch Subtraktion ebenfalls einen Vektor. Beide Ports benötigen wir ohnehin zur Bestimmung des zurückgelegten Weges (Abstand). Wenn das Auto vorwärts fährt zeigt dieser Vektor in die gleiche Richtung wie der Vektor V3, wenn das Auto rückwärts fahrt zeigt der Vektor in die entgegengesetzte Richtung.
Um diese beiden Fälle zu unterscheiden berechnen wir den Winkel zwischen diesen beiden Vektoren. Diese XGroup liefert als Ergebnis den Cosinus des Winkels. Die komplette XPresso-Expressions sieht dann so aus.

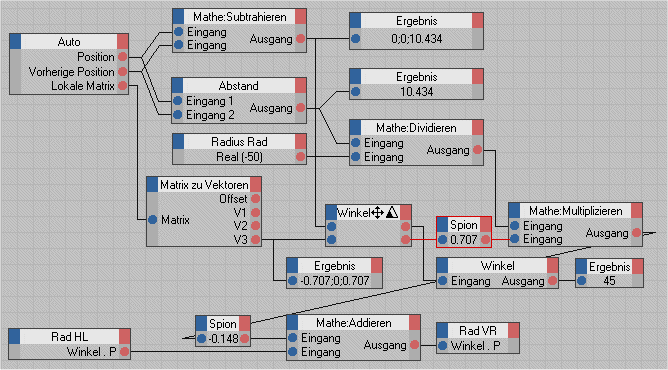
Diesen Cosinus multiplizieren wir mit dem Winkel den wir zum Winkel des Rades addieren. Durch die Änderung des Vorzeichens berücksichtigen wir so die Fahrtrichtung des Autos. Je nach Winkel können wir verschiedene Fälle unterscheiden.

In diesem Fall stimmt die Fahrtrichtung des Autos (Vektor V3) exakt mit der Bewegungsrichtung des Autos überein. Der Cosinus ist positiv, d.h. das Auto fährt vorwärts. Die Bewegung des Autos wird vollständig in eine Drehbewegung des Rades umgesetzt.

In diesem Fall stimmt die Fahrtrichtung des Autos (Vektor V3) nicht mit der Bewegungsrichtung des Autos überein. Der Cosinus ist positiv, d.h. das Auto fährt vorwärts. Nur der Anteil der Bewegung die in Fahrtrichtung erfolgt wird in eine Drehbewegung des Rades umgesetzt.

In diesem Fall stehen die beiden Vektoren senkrecht aufeinander d.h. das Auto wird quer zur Fahrtrichtung (mit quietschenden Reifen) geschoben. Die Räder drehen sich nicht.

In diesem Fall stimmt die Fahrtrichtung des Autos (Vektor V3) nicht mit der Bewegungsrichtung des Autos überein. Der Cosinus ist negativ, d.h. das Auto fährt rückwärts. Nur der Anteil der Bewegung die in Fahrtrichtung erfolgt wird in eine Drehbewegung des Rades umgesetzt.

In diesem Fall ist die Fahrtrichtung des Autos (Vektor V3) entgegengesetzt zur Bewegungsrichtung des Autos. Der Cosinus ist negativ, d.h. das Auto fährt rückwärts. Die Bewegung des Autos wird vollständig in eine Drehbewegung des Rades umgesetzt.

Zur Verdeutlichung noch zwei Skizzen. Im ersten Fall liegen die Fahrtrichtung des Autos (blauer Pfeil) und die Bewegungsrichtung des Autos (roter Pfeil) auf einer Linie. Beide Vektoren zeigen in entgegengesetzte Richtung (phi = 180°) d.h. das Auto fährt rückwärts.

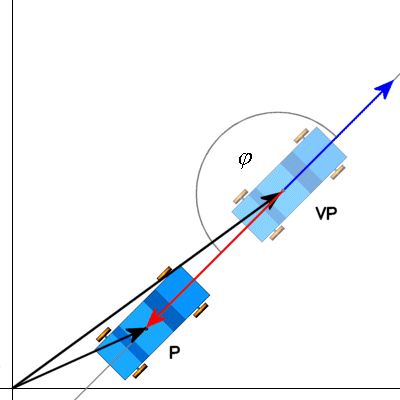
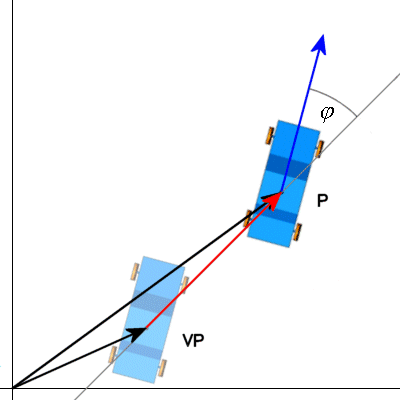
Im zweiten Fall stimmt die Fahrtrichtung des Autos nicht mit der Bewegungsrichtung überein (phi = 30°), d.h. das Auto driftet mit quietschenden Reifen über den Asphalt.

[zurück]

[Inhaltsverzeichnis XPressostoffe]

[vor]