| [zurück] | 3.93. Oloid |
[vor] |
Der (oder das) Oloid [29,30,31] wurde von Paul Schatz (1898 - 1979) entwickelt. Die Basis für den Oloid bilden zwei Scheiben die um 90 ° versetzt ineinander gesteckt werden (siehe Abb. 100).
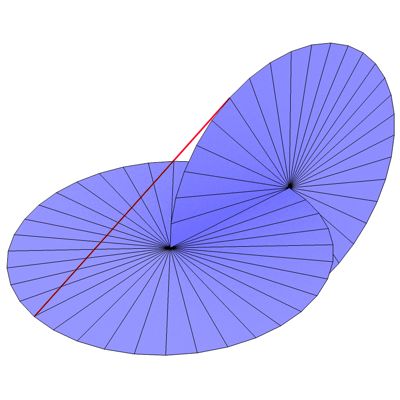
Abb. 100
Die beiden Scheiben sind um den Radius r versetzt. Die rote Gerade zeigt die Verbindungslinie von der einen Scheibe zur anderen. Der Winkel zur horizontalen Scheibe beträgt 30°. Nach dem Satz von Pythagoras läßt sich die Länge der Geraden leicht berechnen.
|
|
3-279 |
|
|
|
3-280 |
Von den beiden Scheiben benötigen wir nur einen Ausschnitt von 240°. In Abb. 101 sind die Scheiben mit den 4 Hauptverbindungslinien als Punkte dargestellt.
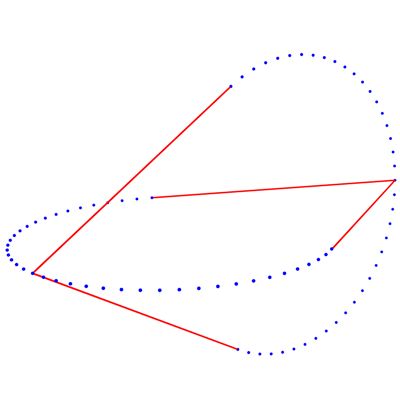
Abb. 101
Für den Oloid lassen sich wahrscheinlich keine parametrischen Gleichungen konstruieren die das komplette Objekt beschreiben. Die beiden Kreisausschnitte können wir aber parametrisch erzeugen.
|
x = 0 |
3-281 |
|
|
y = sin(u) |
3-282 |
|
|
z = 1+cos(u) |
3-283 |
|
|
x = sin(u) |
3-284 |
|
|
y = 0 |
3-285 |
|
|
z = -cos(u) |
3-286 |
Zur Darstellung der Kreisausschnitte muss der Parameter u folgende Werte (Definitionsbereich) annehmen.
|
u ist Element aus der Zahlenmenge [-2 pi/3, 2 pi/3] |
Nun verbinden wir wie in Abb. 101 alle Punkte der einem Scheibe mit den entsprechenden Punkten der anderen Scheibe und erzeugen daraus Polygone. So erhalten wir ein schönes Objekt.

Abb. 102
Abb. 103 zeigt die Draufsicht und Abb. 104 die Seitenansicht des Objektes.
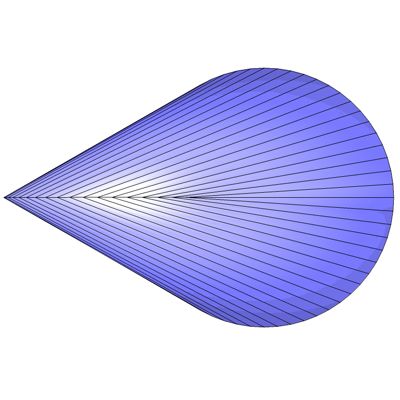
Abb. 103
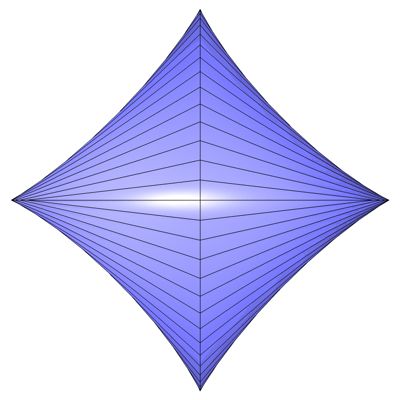
Abb. 104
Bei dieser Figur handelt es sich leider nicht um einen Oloid. Die Verbindungslinien sind unterschiedlich lang, nach der Theorie [30] müssen sie aber alle eine Länge von 1,7321 r haben. Deshalb nennen wir dieses Objekt einfach Pseudo-Oloid.
Beim Pseudo-Oloid handelt es sich um eine geschlossene Figur, der Definitionsbereich kann daher beim Plugin nicht verändert werden.
Das Plugin erzeugt ein optimiertes Mesh ohne doppelte Punkte und nichtverbundene Polygone.
Die Figur kann auf der nächsten Seite mit einem Java-Applet von allen Seiten betrachtet und gedreht werden.
| [zurück] | [Inhaltsverzeichnis] | [vor] |