| [zurück] | 3.139. Epizykloid Torus I |
[vor] |
Der Epizykloid Torus I wird durch folgende Gleichungen dargestellt.
|
x = (R1 + (R + r) cos(v) - h cos(((R + r)/r) v)) cos(u) |
3-448 |
|
|
y = (R + r) sin(v) - h sin(((R + r)/r) v) |
3-449 |
|
|
z = (R1 + (R + r) cos(v) - h cos(((R + r)/r) v)) sin(u) |
3-450 |
Die Konstanten R1, R, r und h bestimmen das Aussehen der Figur.
Zur Darstellung der Fläche können die beiden Parameter u und v zum Beispiel folgende Werte (Definitionsbereich) annehmen.
|
u ist Element aus der Zahlenmenge [0, 2 pi] |
||
|
v ist Element aus der Zahlenmenge [0, 2 pi] |
Da es sich beim Epizykloid Torus I um eine geschlossene Figur handelt muss der Definitionsbereich exakt eingehalten werden, er kann
beim Plugin nicht verändert werden.
Das Plugin erzeugt ein optimiertes Mesh ohne doppelte Punkte und nichtverbundene Polygone.

R/r = 5; r = h
Abb. 200
Die Figur kann auf der nächsten Seite mit einem Java-Applet von allen Seiten betrachtet und gedreht werden.
Der Epizykloid Torus I ist eine Abwandlung des normalen Torus bei dem der kreisförmige Querschnitt durch eine Epizykloide ersetzt wurde.
Die Epizykloide wird durch folgende Gleichungen dargestellt.
|
x = (R + r) cos(t) - h cos(((R + r)/r) t) |
3-451 |
|
|
y = (R + r) sin(t) - h sin(((R + r)/r) t) |
3-452 |
Je nach Wahl der Konstanten kann die Epizykloide verschiedene Formen annehmen. Bei Abb. 201 gilt r = h.
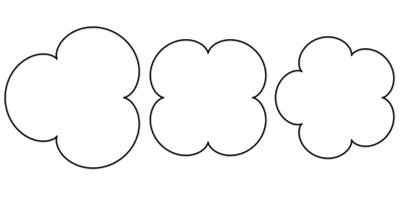
R/r = 3![]() R/r = 4
R/r = 4![]() R/r = 5
R/r = 5
Abb. 201
Bei Abb. 202 gilt R/r = 3.

r > h![]() r = h
r = h![]() r < h
r < h
Abb. 202
Weitere Informationen zur Epizykloide gibt es in meinem Formelspline Tutorial.
| [zurück] | [Inhaltsverzeichnis] | [vor] |