[zurück]

31. Hata Tree

[vor]

Diese Formel habe ich hier [11, 17] gefunden.

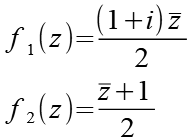
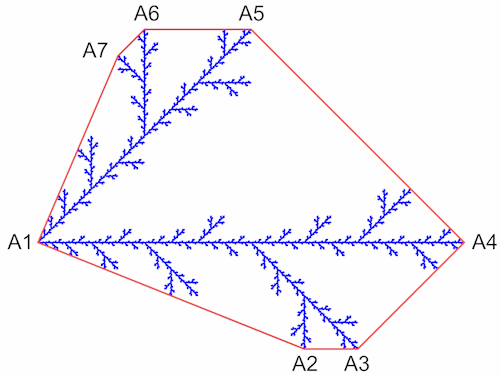
In der folgenden Abbildung wurde jeder Funktion eine Farbe zugewiesen.

Die Eckpunkte der Kurve sind exakt definiert [17].

Die einzelnen Punkte lassen sich auch durch Einsetzten in die Grundgleichung definieren.

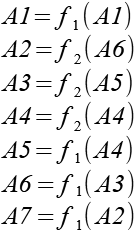
Ich habe dann auch noch die fehlenden Kombinationen ausprobiert und man erhält weitere Endpunkte (A) und einen Verzweigungspunkt (B1). Dem Verzweigungspunkt widme ich mich später.

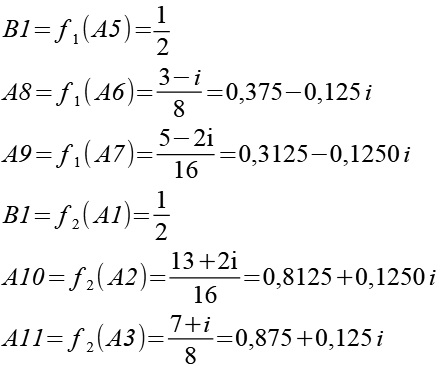
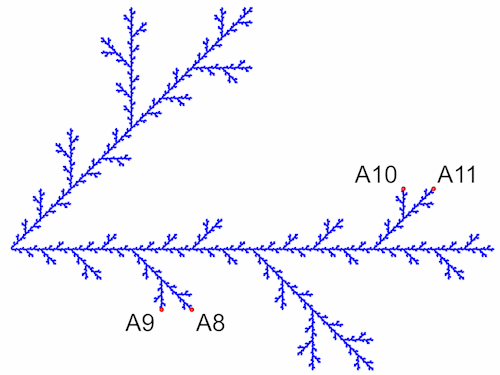
Die neu entstandenen Endpunkte (A8 - A11) habe ich wieder in die Grundgleichung eingesetzt.

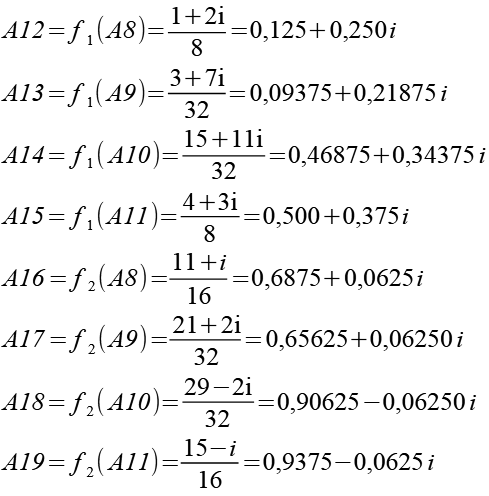
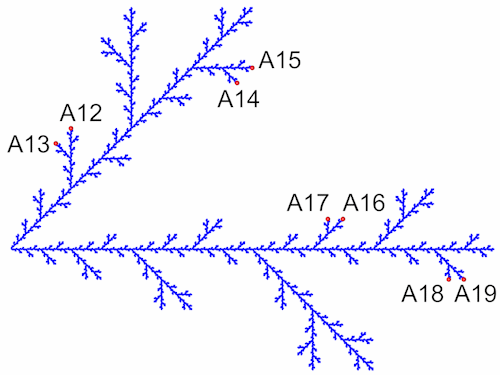
Die neu entstandenen Endpunkte (A12 - A19) habe ich wieder in die Grundgleichung eingesetzt.

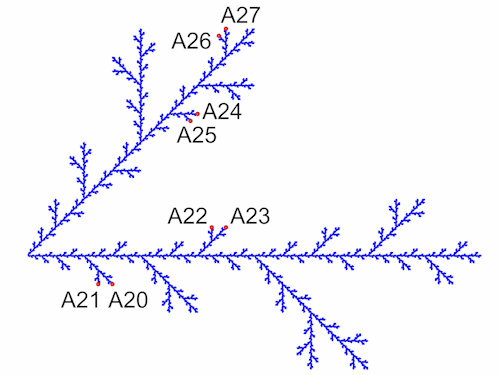
Die neu entstandenen Endpunkte (A20 - A27) habe ich wieder in die Grundgleichung eingesetzt.

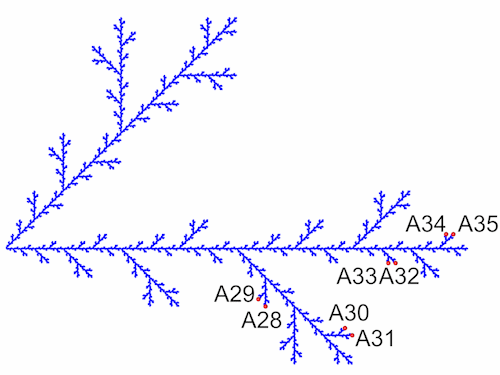
Die neu entstandenen Endpunkte (A28 - A35) habe ich wieder in die Grundgleichung eingesetzt.

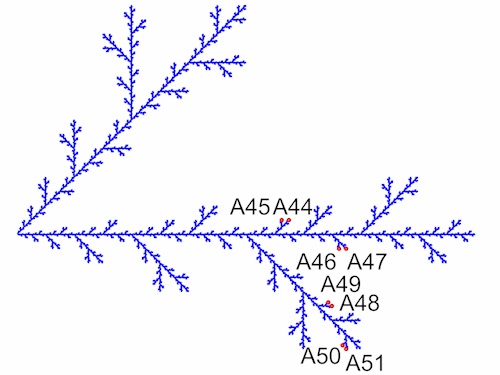
Die neu entstandenen Endpunkte (A36 - A43) habe ich wieder in die Grundgleichung eingesetzt.

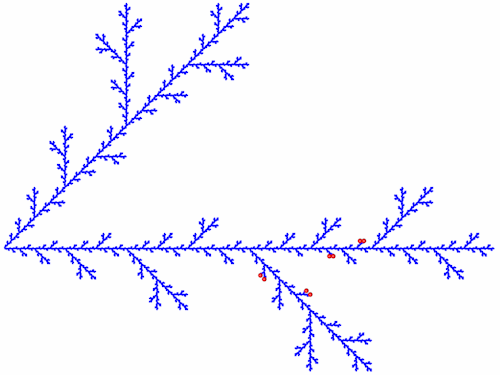
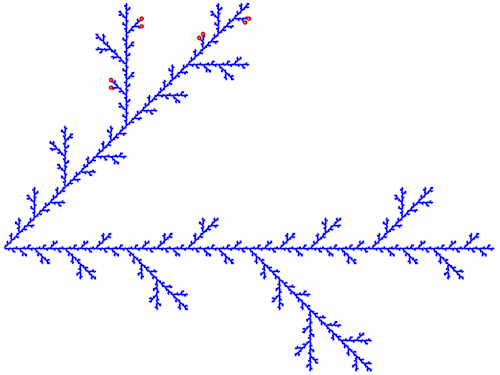
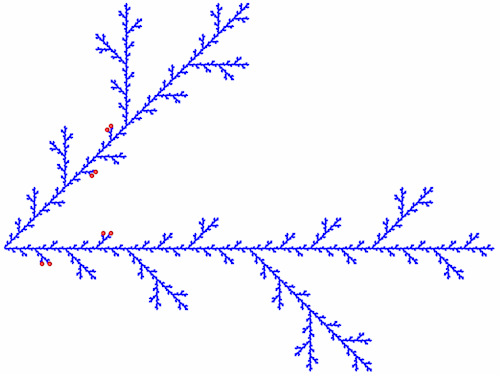
Die neu entstandenen Endpunkte (A44 - A51) habe ich wieder in die Grundgleichung eingesetzt.

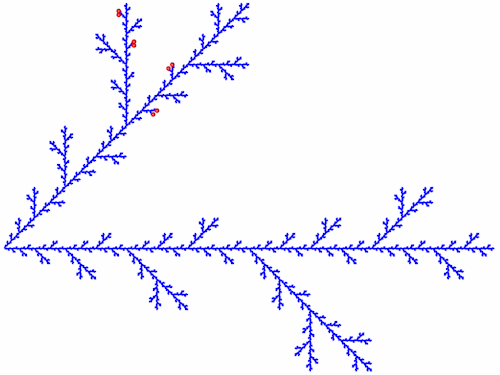
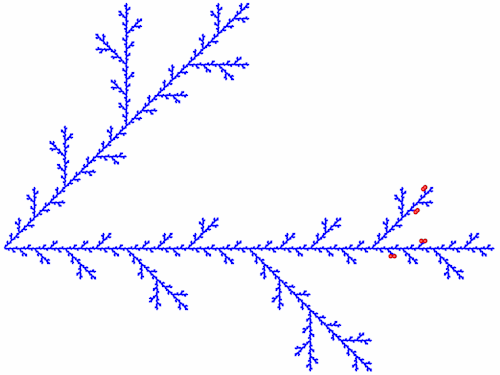
In der folgenden Abbildung sind alle Punkte von A1 bis A99 dargestellt.

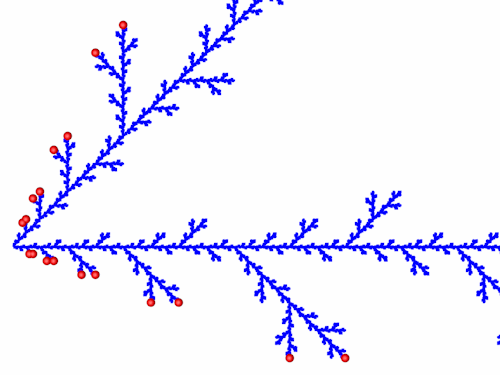
Die Endpunkte treten bei der Berechnung immer als benachbarte Pärchen auf. An Hand von zwei Beispielen habe ich versucht das zu analysieren. Als erstes Beispiel habe ich die Punkte A6 und A7 in Funktion f₁ eingesetzt. Zur bessere Übersicht habe ich die neuen Punkte D und E genannt.

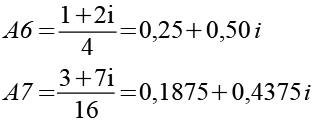
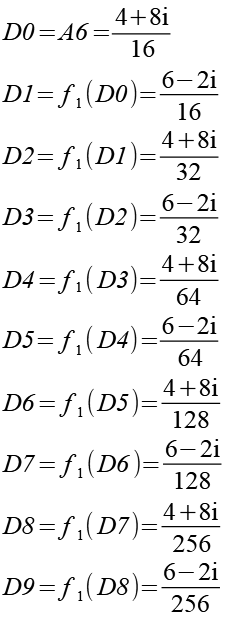
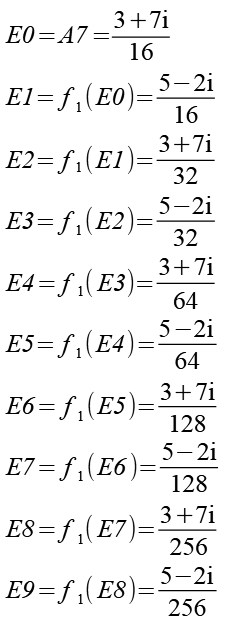
Der Zähler der Brüche bleibt konstant und wechselt alternierent, der Nenner verdoppelt sich. Die Formel für die Punkte läßt sich auch allgemein ausdrücken.

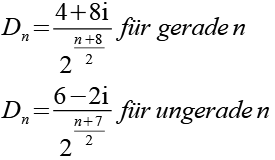
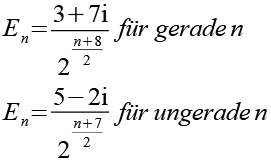
Als zweites Beispiel habe ich die Punkte A8 und A9 in Funktion f₂ eingesetzt. Zur bessere Übersicht habe ich die neuen Punkte F und G genannt.

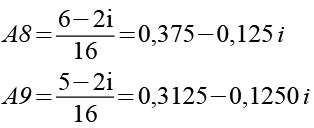
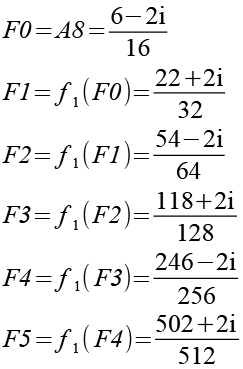
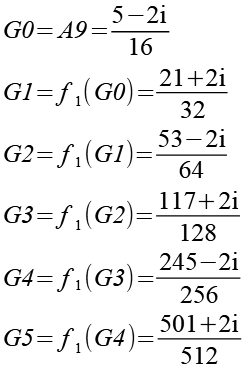
Die Formel für die Punkte läßt sich auch allgemein ausdrücken.

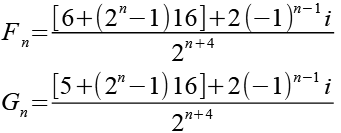
Auf dem unteren Ast des Hata Tree`s gibt es vier Pärchen auf gleicher Höhe, die habe ich mir genauer angesehen.

Es sind die Punkte A34/A35, A40/A41, A44/A45 und A70/A71, ich habe sie nach der Größe sortiert und neu nummeriert (H ind I).

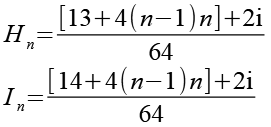
[zurück]

[Inhaltsverzeichnis]

[vor]