| [zurück] | 4. Lucas Folgen |
[vor] |
Die Lucas Folgen basieren auf den gleichen Gesetzmäßigkeiten wie die Fibonacci Zahlen, nur die Startwerte sind anders.
Folge 1
![]()
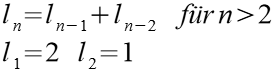
| n | ln | n | ln | |
| 1 | 2 | 11 | 123 | |
| 2 | 1 | 12 | 199 | |
| 3 | 3 | 13 | 322 | |
| 4 | 4 | 14 | 521 | |
| 5 | 7 | 15 | 843 | |
| 6 | 11 | 16 | 1364 | |
| 7 | 18 | 17 | 2207 | |
| 8 | 29 | 18 | 3571 | |
| 9 | 47 | 19 | 5778 | |
| 10 | 76 | 20 | 9349 |
Aus den Lucas Zahlen läßt sich wie bei den Fibonacci Zahlen der goldene Schnitt ableiten. Dazu bilden wir den Quotienten zweier benachbarter Zahlen. Je größer die Zahlen desto genauer ist das Ergebnis.
| ln | ln-1 | ln/ln-1 |
| 7 | 4 | 1,7500 |
| 11 | 7 | 1,5714 |
| 18 | 11 | 1,6364 |
| 29 | 18 | 1,6111 |
| 47 | 29 | 1,6207 |
| 76 | 47 | 1,6170 |
| 123 | 76 | 1,6184 |
| 199 | 123 | 1,6179 |
| 322 | 199 | 1,6181 |
| 521 | 322 | 1,6180 |
| 843 | 521 | 1,6180 |
Folge 2
![]()
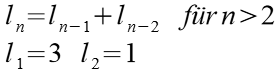
| n | ln | n | ln | |
| 1 | 3 | 11 | 157 | |
| 2 | 1 | 12 | 254 | |
| 3 | 4 | 13 | 411 | |
| 4 | 5 | 14 | 665 | |
| 5 | 9 | 15 | 1076 | |
| 6 | 14 | 16 | 1741 | |
| 7 | 23 | 17 | 2817 | |
| 8 | 37 | 18 | 4558 | |
| 9 | 60 | 19 | 7375 | |
| 10 | 97 | 20 | 11933 |
Aus den Lucas Zahlen läßt sich wie bei den Fibonacci Zahlen der goldene Schnitt ableiten. Dazu bilden wir den Quotienten zweier benachbarter Zahlen. Je größer die Zahlen desto genauer ist das Ergebnis.
| ln | ln-1 | ln/ln-1 |
| 9 | 5 | 1,7500 |
| 14 | 9 | 1,5556 |
| 23 | 14 | 1,6429 |
| 37 | 23 | 1,6087 |
| 60 | 37 | 1,6216 |
| 97 | 60 | 1,6167 |
| 157 | 97 | 1,6186 |
| 254 | 157 | 1,6178 |
| 411 | 254 | 1,6181 |
| 665 | 411 | 1,6180 |
| 1076 | 665 | 1,6180 |
Folge 3
![]()
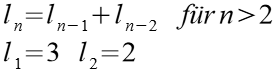
| n | ln | n | ln | |
| 1 | 3 | 11 | 212 | |
| 2 | 2 | 12 | 343 | |
| 3 | 5 | 13 | 555 | |
| 4 | 7 | 14 | 898 | |
| 5 | 12 | 15 | 1453 | |
| 6 | 19 | 16 | 2351 | |
| 7 | 31 | 17 | 3804 | |
| 8 | 50 | 18 | 6155 | |
| 9 | 81 | 19 | 9959 | |
| 10 | 131 | 20 | 16114 |
Aus den Lucas Zahlen läßt sich wie bei den Fibonacci Zahlen der goldene Schnitt ableiten. Dazu bilden wir den Quotienten zweier benachbarter Zahlen. Je größer die Zahlen desto genauer ist das Ergebnis.
| ln | ln-1 | ln/ln-1 |
| 7 | 5 | 1,4000 |
| 12 | 7 | 1,7143 |
| 19 | 12 | 1,5833 |
| 31 | 19 | 1,6316 |
| 50 | 31 | 1,6129 |
| 81 | 50 | 1,6200 |
| 131 | 81 | 1,6173 |
| 212 | 131 | 1,6179 |
| 343 | 212 | 1,6179 |
| 555 | 343 | 1,6181 |
| 898 | 555 | 1,6180 |
Folge 4
![]()
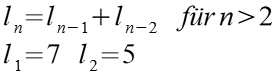
| n | ln | n | ln | |
| 1 | 7 | 11 | 513 | |
| 2 | 5 | 12 | 830 | |
| 3 | 12 | 13 | 1343 | |
| 4 | 17 | 14 | 2173 | |
| 5 | 29 | 15 | 3516 | |
| 6 | 46 | 16 | 5689 | |
| 7 | 75 | 17 | 9205 | |
| 8 | 121 | 18 | 14894 | |
| 9 | 196 | 19 | 24099 | |
| 10 | 317 | 20 | 38993 |
Aus den Lucas Zahlen läßt sich wie bei den Fibonacci Zahlen der goldene Schnitt ableiten. Dazu bilden wir den Quotienten zweier benachbarter Zahlen. Je größer die Zahlen desto genauer ist das Ergebnis.
| ln | ln-1 | ln/ln-1 |
| 17 | 12 | 1,4167 |
| 29 | 17 | 1,7059 |
| 46 | 29 | 1,5862 |
| 75 | 46 | 1,6304 |
| 121 | 75 | 1,6133 |
| 196 | 121 | 1,6198 |
| 317 | 196 | 1,6173 |
| 513 | 317 | 1,6183 |
| 830 | 513 | 1,6179 |
| 1343 | 830 | 1,6181 |
| 2173 | 1343 | 1,6180 |
Folge 5
![]()
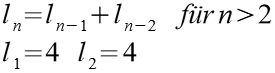
| n | ln | n | ln | |
| 1 | 4 | 11 | 356 | |
| 2 | 4 | 12 | 576 | |
| 3 | 8 | 13 | 932 | |
| 4 | 12 | 14 | 1508 | |
| 5 | 20 | 15 | 2440 | |
| 6 | 32 | 16 | 3948 | |
| 7 | 52 | 17 | 6388 | |
| 8 | 84 | 18 | 10336 | |
| 9 | 136 | 19 | 16724 | |
| 10 | 220 | 20 | 27060 |
Aus den Lucas Zahlen läßt sich wie bei den Fibonacci Zahlen der goldene Schnitt ableiten. Dazu bilden wir den Quotienten zweier benachbarter Zahlen. Je größer die Zahlen desto genauer ist das Ergebnis.
| ln | ln-1 | ln/ln-1 |
| 12 | 8 | 1,5000 |
| 20 | 12 | 1,6667 |
| 32 | 20 | 1,6000 |
| 52 | 32 | 1,6250 |
| 84 | 52 | 1,6154 |
| 136 | 84 | 1,6190 |
| 220 | 136 | 1,6176 |
| 356 | 220 | 1,6182 |
| 576 | 356 | 1,6180 |
| 932 | 576 | 1,6181 |
| 1508 | 932 | 1,6180 |
Folge 6
![]()
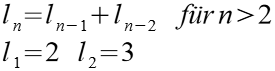
| n | ln | n | ln | |
| 1 | 2 | 11 | 233 | |
| 2 | 3 | 12 | 377 | |
| 3 | 5 | 13 | 610 | |
| 4 | 8 | 14 | 987 | |
| 5 | 13 | 15 | 1597 | |
| 6 | 21 | 16 | 2584 | |
| 7 | 34 | 17 | 4181 | |
| 8 | 55 | 18 | 6765 | |
| 9 | 89 | 19 | 10946 | |
| 10 | 144 | 20 | 17711 |
Aus den Lucas Zahlen läßt sich wie bei den Fibonacci Zahlen der goldene Schnitt ableiten. Dazu bilden wir den Quotienten zweier benachbarter Zahlen. Je größer die Zahlen desto genauer ist das Ergebnis.
| ln | ln-1 | ln/ln-1 |
| 5 | 3 | 1,6667 |
| 8 | 5 | 1,6000 |
| 13 | 8 | 1,6250 |
| 21 | 13 | 1,6154 |
| 34 | 21 | 1,6190 |
| 55 | 34 | 1,6176 |
| 89 | 55 | 1,6182 |
| 144 | 89 | 1,6180 |
| 233 | 144 | 1,6181 |
| 377 | 233 | 1,6180 |
| 610 | 377 | 1,6180 |
Folge 7
![]()
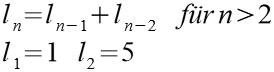
| n | ln | n | ln | |
| 1 | 1 | 11 | 309 | |
| 2 | 5 | 12 | 500 | |
| 3 | 6 | 13 | 809 | |
| 4 | 11 | 14 | 1309 | |
| 5 | 17 | 15 | 2118 | |
| 6 | 28 | 16 | 3427 | |
| 7 | 45 | 17 | 5545 | |
| 8 | 73 | 18 | 8972 | |
| 9 | 118 | 19 | 14517 | |
| 10 | 191 | 20 | 23489 |
Aus den Lucas Zahlen läßt sich wie bei den Fibonacci Zahlen der goldene Schnitt ableiten. Dazu bilden wir den Quotienten zweier benachbarter Zahlen. Je größer die Zahlen desto genauer ist das Ergebnis.
| ln | ln-1 | ln/ln-1 |
| 11 | 6 | 1,8333 |
| 17 | 11 | 1,5455 |
| 28 | 17 | 1,6471 |
| 45 | 28 | 1,6071 |
| 73 | 45 | 1,6222 |
| 118 | 73 | 1,6164 |
| 191 | 118 | 1,6186 |
| 309 | 191 | 1,6178 |
| 500 | 309 | 1,6181 |
| 809 | 500 | 1,6180 |
| 1309 | 809 | 1,6180 |
| [zurück] | [Inhaltsverzeichnis] | [vor] |