| [zurück] | Peaucellier Geradführung |
[vor] |
Bei der Peaucellier Geradführung wird die Drehbewegung in eine exakte Gerade umgewandelt. Sie wurde von Charles-Nicolas Peaucellier (1832 - 1913) entdeckt.
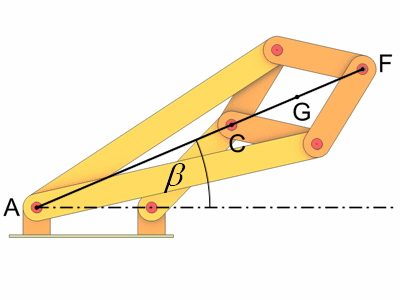
Die Peaucellier Geradführung besteht aus 8 Stäben die durch Gelenke miteinander verbunden sind. Die Stäbe werden wie folgt definiert.
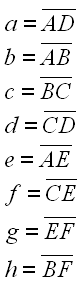 |
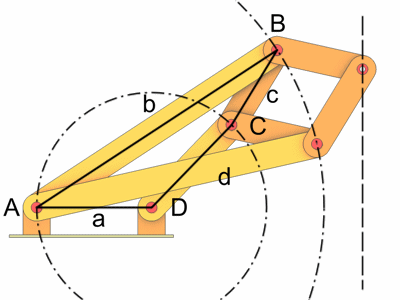
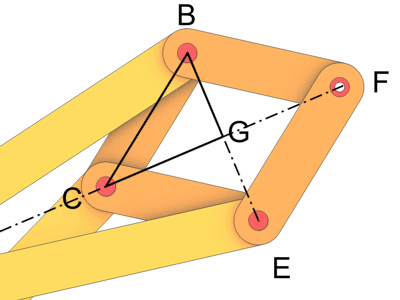
Das Gelenkviereck ABCD läßt sich einfach animieren (siehe Doppelschwinge). Die Drehung der Kurbel d wird in eine geradlinige Bewegung des Punktes F umgewandelt. Die Stäbe c, f, g und h sind gleich lang und bilden eine Raute (BCEF).
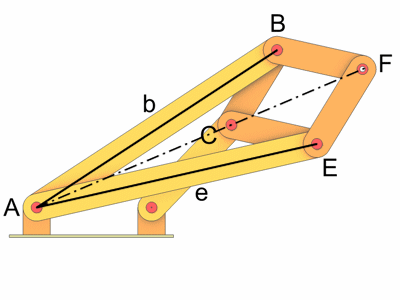
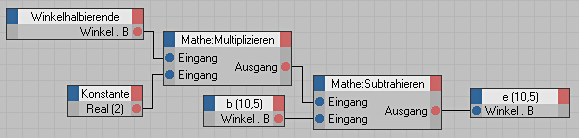
Um den Stab e zu positionieren benutzen wir die Linie ACF. Sie bildet die Winkelhalbierende bzw. Symmetrieachse für b und e. Um den Winkel der Winkelhalbierenden zu bestimmen erzeugen wir in Cinema ein Hilfsobjekt. Das könnte ein Nullobjekt sein aber wir nehmen ein Spline damit die Linie im Editor sichtbar ist. Die Objektachse der Winkelhalbierenden positionieren wir in Punkt A und richten sie mit einem Constraint auf den Punkt C aus. Aus dem Winkel des Stabes b und dem Winkel der Winkelhalbierenden können wir den Winkel des Stabes e berechnen.
Jetzt können wir Stab f einbauen, wir positionieren ihn auf Punkt C und richten ihn auf Punkt E aus.
Jetzt fehlt noch Punkt F, um seine Position zu berechnen beutzen wir einen Trick. Wir betrachten zuerst die Raute BCEF und ziehen eine Hilfslinie von B zu E. Die Länge dieser Strecke a2 berechnen wir mit dem Abstand Node. Zusätzlich benötigen wir noch den Abstand a1 von Punkt A und Punkt C.
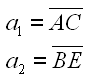 |
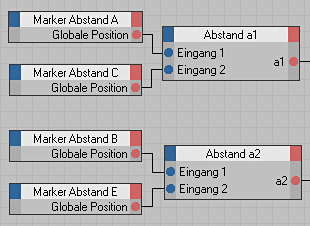
Diese Linie schneidet die Winkelhalbierende im Punkt G. Die Punkte B, C und G bilden ein rechtwinkliges Dreieck. Die Seite c des Dreiecks ist bekannt und nach dem Satz von Pythagoras läßt sich die Seite c1 berechnen.
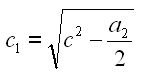 |
So können wir jetzt die Entfernung der Punkte A und F berechnen.
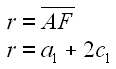 |

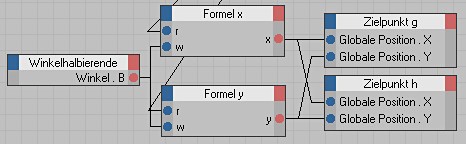
Mit der Strecke r und dem Winkel beta haben wir die Polarkoordinaten des Punktes F. Um den Zielpunkt zu berechnen wandeln wir die Polarkoordinaten in kartesische Koordinaten um. Für die beiden Stäbe g und h gibt es separate Zielpunkte das sie sich in der z Koordinate unterscheiden.
Download C4D Datei (Release 11) : Peaucellier.zip
| [zurück] | [Inhaltsverzeichnis] | [vor] |