| [zurück] | 3.1. 8 Tetraeder |
[vor] |
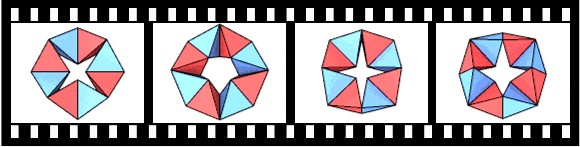
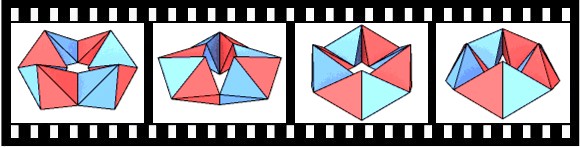
Unter Kaleidozyklen versteht man einen Ring aus Tetraedern die zu einem Ring verbunden sind. Die Tetraeder sind an jeweils 2 Kanten miteinander verbunden, die Kanten fungieren als Scharnier. Diesen Ring kann man in sich drehen ohne das die Verbindung der Tetraeder untereinander verloren geht.
Wer sich über dieses Thema informieren möchte sollte einen Blick auf die Seiten Mathematische Basteleien oder Kaleidocycles werfen.
So ein Ring läßt sich auch als Papiermodell aus einen Schnittmusterbogen bauen. Das Prinzip dieser Ringe läßt am besten dadurch begreifen das man ihn in der Hand dreht.
Bei diesem Beispiel handelt es sich um einen Ring aus 8 regulären Tetraedern die jeweils aus 4 gleichseitigen Dreiecken bestehen.
Die Bildgröße beträgt 352*288 Pixel, das Format ist MPEG1. Die unterschiedliche Texturierung dient nur zu besseren Übersicht, alle 8 Tetraeder sind gleich.
Die Animationen habe ich in Cinema mit XPresso realisiert. Die dafür nötigen Formeln stammen aus einem Mathematica Skript von Maurice Starck. Jeder Punkt der Tetraeder wird durch eine eigene Formel animiert die z.B. so aussieht.
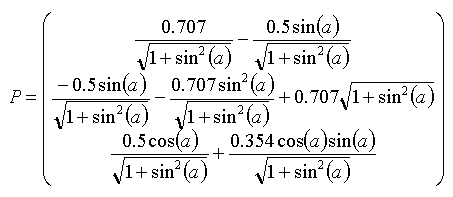
Die mathematische Theorie dazu findet man bei Kaleidocycles.
Download Cinema Datei (Version 8) : Kaleido-8.zip
| [zurück] | [Inhaltsverzeichnis] | [vor] |