| [zurück] | Versiera der Agnesi |
[vor] |
Die Versiera der Agnesi (oder Witch of Agnesi) wurde 1748 von Maria Agnesi beschrieben.
Die Parameterdarstellung lautet.
|
X(t) = 2 * a * t |
1-38 |
|
|
Y(t) = 2 * a / (1 + t2) |
1-39 |
oder
|
X(t) = 2 * a / tan(t * pi) |
1-40 |
|
|
Y(t) = a * (1 – cos(2 * t * pi)) |
1-41 |
Auch eine normale Darstellung der Funktion ist möglich.
|
y = 8 * a3 / (x2 + 4 * a2) |
1-42 |
Bei x = 0 besitzt die Funktion ein Maximum (y = 2 * a). Zeichnet man die Stelle (x = 0, y = a) einen Kreis mit dem Radius a so schmiegt sich die Kurve optimal an den Kreis, wie eine Tischdecke die auf einem Ball liegt.
Abb. 10 wurde mit den Gleichungen 1-38/39 berechnet.
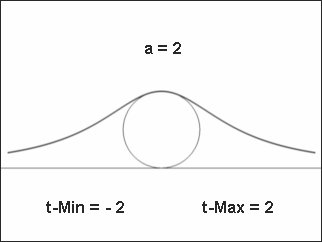
Abb. 10
| [zurück] | [Inhaltsverzeichnis] | [vor] |